Introduction

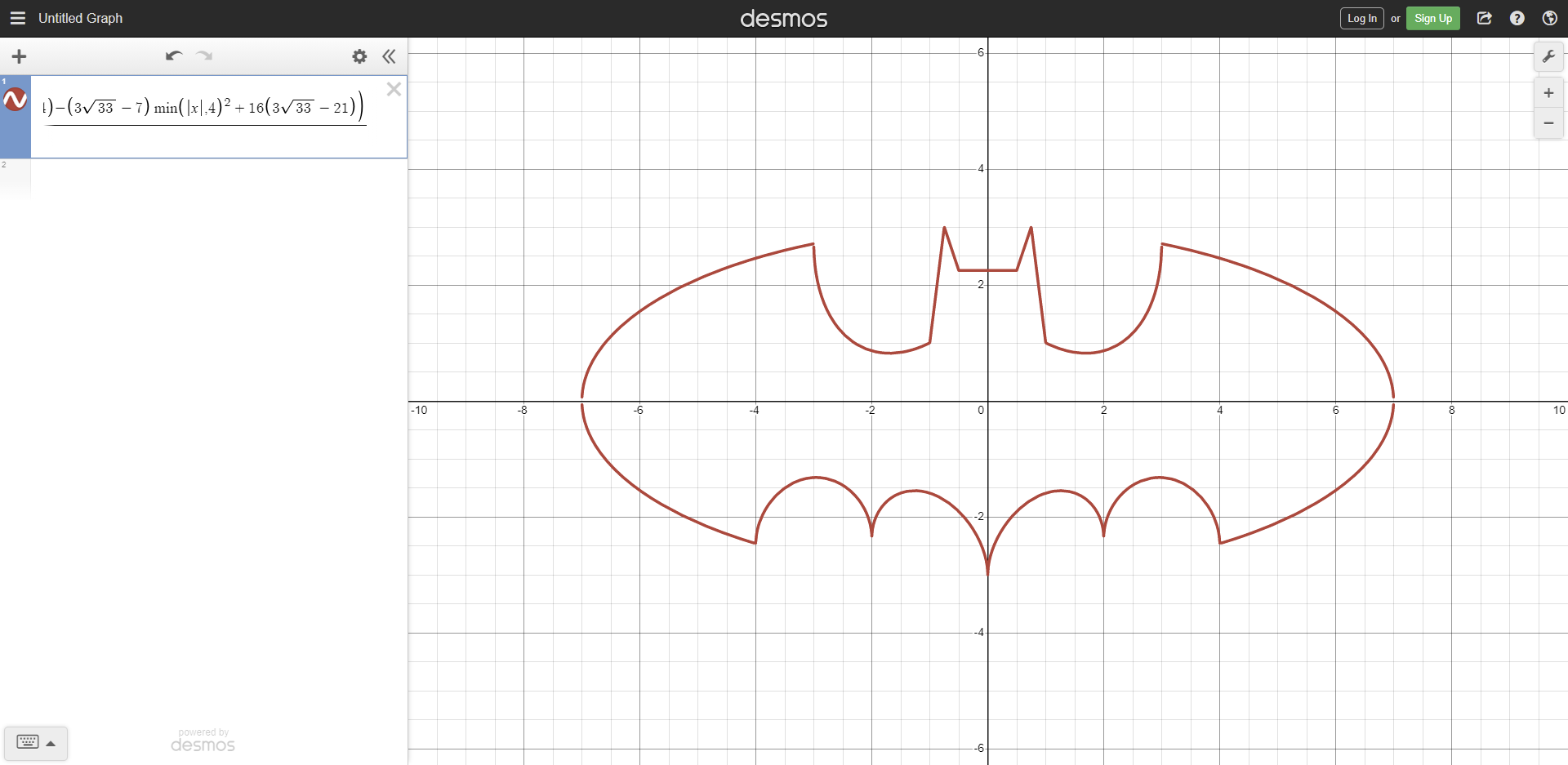
I have no idea how to start this post off to be honest. I'm feeling so many things at the moment. It's funny though, because at the time of writing, I've just finished reconstructing the batman equation. Yeah, this batman equation. By the end of this post, you'll hopefully understand one of the techniques for constructing it, even if you don't know the formula (click to expand). It is shown below:

And in action:

Why, you might ask, would I create such a preposterous equation - one that already has an equation, mind you? Well firstly, ever since I first saw the batman equation, I wanted to understand how it worked. How I might be able to create something so cool, or even, recreate it myself. Likewise, ever since my work begun on piecewise equations, I realised the crudeness of taking the root of a signum or 'pseudo-signum' (\(\frac{|x|}{x}\)) to limit the equation. Don't get me wrong - it is an absolutely brilliant idea, but it comes with pitfalls:

• A lot of graphing calculators apply the restrictions everywhere - even when the null factor law is applied. This prevents multiple equations from being 'stuck together' as it were, because you're limited to a certain area.
• Using what I colloquially call a pseudo-signum causes the equation to be undefined wherever that signum would normally zero. These undefined points destroy continuity, which, while I normally wouldn't care too much about, is ideal when making an object like the batman equation.
• It's messy. Well, so's mine.

Conversely, that same technique:

• Can easily and simply 'cut' a function or relation to a single region or line.
• Is easy to 'plug in'.
• Is a beautiful demonstration of the properties of absolute value and interactions with functions that become undefined for certain values.

So what's this post about? Combining equations/functions. We want to stick as many functions together along some function (in this post, will be \(x\)), and will do so, using the answer to the question I posed a little bit ago in questions. Do notice I'm leaving the notion of combining relations open - it is possible, but not something we'll at all touch on in this post.

Combining two functions - and more

Suppose we want a continuous function such that \(f_1\) is plotted before, and at, \(x=x_1\), and \(f_2\) plotted after and at same said point. We then have the following function:

\[ f(x) = \begin{cases} f_1(x) & x\leq x_1 \\ f_2(x) & x\geq x_1 \end{cases}\]

The way we can come up with a 'proper' function for this (closed, proper, don't know what to call it - but a function that expresses itself without reference to piecewise notation - max(a,b), min(a,b) and abs(x) are such functions) is highly unintuitive, but we can ultimately do the following:

\[ \begin{align} f(x) &= \begin{cases} f_1(x) & x\leq x_1 \\ f_2(x) & x\geq x_1 \end{cases} \\ &= \begin{cases} f_1(x) & x< x_1 \\ 0 & x\geq x_1 \end{cases}+ \begin{cases} 0 & x\leq x_1 \\ f_2(x) & x> x_1 \end{cases} \\ &= \begin{cases} f_1(x) & x< x_1 \\ f_1(x_1) & x\geq x_1 \end{cases}+ \begin{cases} f_2(x_1) & x\leq x_1 \\ f_2(x) & x> x_1 \end{cases} - \begin{cases} f_2(x_1) & x\leq x_1 \\ f_1(x_1) & x\geq x_1 \end{cases} \\ &= f_1(\min(x,x_1)) + f_2(\max(x,x_1)) - \begin{cases} f_2(x_1) & x\leq x_1 \\ f_2(x_1) & x\geq x_1 \end{cases} \\ &= f_1(\min(x,x_1)) + f_2(\max(x,x_1)) - f_2(x_1) \\ \end{align}\]

And we've found a nice form (you can expand by max, min and abs definitions for piecewise-less fun). What's even nicer is that we can apply this to three equations in a similar way by the following (where \(x_1\leq x_2\)):

\[ \begin{align} f(x) &= \begin{cases} f_1(x) & x\leq x_1 \\ f_2(x) & x_1\leq x\leq x_2 \\ f_3(x) & x_2 \leq x \end{cases} \\ &= \begin{cases} \begin{cases} f_1(x) & x\leq x_1 \\ f_2(x) & x\geq x_1 \end{cases} & x\leq x_2 \\ f_3(x) & x \geq x_2 \end{cases} \\ &= \begin{cases} f_1(\min(x,x_1))+f_2(\max(x,x_1))-f_2(x_1) & x\leq x_2 \\ f_3(x) & x \geq x_2 \end{cases} \\ &= f_1(\min(\min(x,x_2),x_1))+f_2(\max(\min(x,x_2),x_1))-f_2(x_1) + f_3(\max(x,x_2)) - f_3(x_2) \\ &= f_1(\min(x,x_1))+f_2(\max(\min(x,x_2),x_1))+f_3(\max(x,x_2))-f_2(x_1)- f_3(x_2) \end{align}\]

Cool, hey?

Formula/rule for \(n\) functions

From our previous section and derivation, an interesting pattern seems to emerge. A function \(g\) can be 'added' to \(f\) at a point \(k\) by simply appending to the equation \(g(\max(\min(x,U),L)-g(L)\) where \(L\) is the lower bound, and \(U\) is the upper bound. This, of course, makes sense. In our existing equations, the leftmost and rightmost equations are respectively bounded in \(\mathbb{R}\) by positive/negative infinities, more or less (and so cancel out - really, this is a limit for which N < x or x > N for all x, also).

We thus derive a couple of variations for the formula:

Closed Case Formula

Let \(s\) be a non-decreasing sequence such that \(s=\left\{a,x_1,\dots,x_{n-1},b\right\}\), then for some \(f:[a,b]\to\mathbb{R}\) we have:

\[ f(x)=\sum_{k=1}^{n}{f_{k}(\max(\min(x,s_{k+1}),s_{k}))}-\sum_{k=2}^{n}f_k(s_k)\]

'Open' Case Formula

Let \(s\) be a non-decreasing sequence such that \(s=\left\{-m,x_1,\dots,x_{n-1},m\right\}\), then for some \(f:\mathbb{R}\to\mathbb{R}\) we have:

\[ f(x)=\lim_{m\to\infty}\sum_{k=1}^{n}{f_{k}(\max(\min(x,s_{k+1}),s_{k}))}-\sum_{k=2}^{n}f_k(s_k)\]

Where \(f(x)\) is a combination of functions \(f_1(x),\dots,f_n(x)\) on domains \(\left[a,x_1\right], \left[x_1,x_2\right], \dots, \left[x_{n-1},b\right]\) respectively in the closed case, and the same combination of functions on domains \(\left(-\infty,x_1\right], \left[x_1,x_2\right],\dots, \left[x_{n-1},\infty\right)\) respectively in the open case.

Should also be noted that, given \(u\geq l\), \(\max(\min(x,u),l)=\frac{1}{2}\left(u+l+|x-l|-|x-u|\right)\). If \(l=-u\), then we have \(\frac{1}{2}\left(|x+u|-|x-u|\right)\).

Proof

Let \(P(k), k\geq 2\) be the statement that \(f(x)\) is the functional form for a given piecewise function; namely the following:

\[ \begin{cases} \begin{cases} \begin{matrix} \begin{cases} f_1(x) & x\leq x_1\\ f_2(x) & x\geq x_1 \end{cases} & \dots \\ \vdots & \ddots \end{matrix} & x\leq x_{k-2} \\ f_{k-1}(x) & x\geq x_{k-2} \end{cases} & x\leq x_{k-1} \\ f_k(x) & x\geq x_{k-1} \end{cases}\]

That is, this piecewise function describes each function on their respective intervals as given by the problem. Notice also the piecewise function works in both open and closed cases (the \(x\leq b\) and \(x\geq a\) conditions are implied by the interval restriction on the function, for example).

For our base cases, let \(k=2\) and consider the open case first - wherein \(s=\left\{-n,x_1,n\right\}\):

\[ \begin{align} P(2)&=f_1(\min(x,x_1))+f_2(\max(x,x_1))-f_2(x_1)\\ &=\lim_{n\to\infty} f_1(\max(\min(x,x_1),-n))+f_2(\max(\min(x,n),x_1))-\sum_{k=2}^{2}f_k(s_k)\\ &=\lim_{n\to\infty} \sum_{k=1}^{2}{f_{k}(\max(\min(x,s_{k+1}),s_{k}))}-\sum_{k=2}^{2}f_k(s_k) \end{align}\]

For the closed case, we let \(s=\left\{a,x_1,x_2,b\right\}\) and achieve a similar result (as you can verify yourself), hence proved for the base cases.

Therefore, we have \(P(k)\implies P(k+1)\), and thus for \(P(k+1)\) we have:

\[ \begin{cases} \begin{cases} \begin{matrix} \begin{cases} f_1(x) & x\leq x_1\\ f_2(x) & x\geq x_1 \end{cases} & \dots \\ \vdots & \ddots \end{matrix} & x\leq x_{k-1} \\ f_{k}(x) & x\geq x_{k-1} \end{cases} & x\leq x_{k} \\ f_{k+1}(x) & x\geq x_{k} \end{cases}\]

This is, by our induction hypothesis, equal to, in the open case, where \(s=\left\{-n,x_1,\dots,x_k,n\right\}\):

\[ \begin{cases} \lim_{n\to\infty}\sum_{j=1}^{k}{f_{j}(\max(\min(x,s_{j+1}),s_{j}))}-\sum_{j=2}^{k}f_j(s_j) & x\leq x_{k} \\ f_{k+1}(x) & x\geq x_{k} \end{cases}\]

The same step can be taken for the closed case. Verification of that is left to the reader, but is otherwise a trivial exercise. Continuing, by our original identity this is equal to:

\[ \lim_{n\to\infty}\sum_{j=1}^{k}{f_{j}(\max(\min(\min(x,x_k),s_{j+1}),s_{j}))}-\sum_{j=2}^{k}f_j(s_j)+\\ f_{k+1}(\max(x,x_k))-f_{k+1}(x_k)\]

We have to split the first sum up, given that \(x_k\geq s_{k+1}\). We can otherwise simplify:

\[ \lim_{n\to\infty}\sum_{j=1}^{k-1}{f_{j}(\max(\min(x,s_{j+1}),s_{j}))}-\sum_{j=2}^{k-1}f_j(s_j)+\\ f_{k+1}(\max(x,x_k))-f_{k+1}(x_k)+\\ f_k(\max(\min(x,x_k),s_k))-f_k(s_k)\]

We can now define a new sequence, \(s'=\left\{-n,x_1,\dots,x_{k+1},n\right\}\) so that we can re-index along our new sequence. That is, \(x_k\mapsto s'_{k+1}\), \(s_k\mapsto s'_{k}\) and \(s_{k+1}\mapsto s'_{k+2}\).

\[ \lim_{n\to\infty}\sum_{j=1}^{k-1}{f_{j}(\max(\min(x,s'_{j+1}),s'_{j}))}-\sum_{j=2}^{k-1}f_j(s'_j)+\\ f_{k+1}(\max(x,s_{k+1}))-f_{k+1}(s'_{k+1})+\\ f_k(\max(\min(x,s'_{k+1}),s'_k))-f_k(s'_k)\]

Finally, using \(\max(x,x_{k+1})=\max(\min(x,x_{k+2}),x_{k+1}))\) and recombining all terms:

\[ \lim_{n\to\infty}\sum_{j=1}^{k+1}{f_{j}(\max(\min(x,s'_{j+1}),s'_{j}))}-\sum_{j=2}^{k+1}f_j(s'_j)\]

Hence proved. A similar proof with the same argument follows for the closed case (essentially neglecting the limit).

A note on 'clamping'

Notable mentions: StackExchange, Clamping - stub - Wikipedia, StackExchange, Smoothstep - Wikipedia

Interestingly, the formulas we derived make use of these clamping functions.

Let's denote this clamping function \(\operatorname{clamp}_{a,b}(x)=\max(\min(x,b),a)\). I claimed that, earlier, this function is just \(\frac{1}{2}\left(a+b+|x-a|-|x-b|\right)\). Given that \(b\geq a\), the proof is as follows:

\[ \begin{align} \operatorname{clamp}_{a,b}(x) &= \max(\min(x,b),a) \\ &= \max(a-\min(x,b),0)+\min(x,b) \\ &= -\min(\min(x-a,b-a),0)+\min(x,b) \\ &= a-\min(x,a)+\min(x,b) \\ &= a+\frac{1}{2}\left(x+b-|x-b|-x-a+|x-a|\right) \\ &= \frac{1}{2}\left(a+b+|x-a|-|x-b|\right) \end{align}\]

Typically, in computer science or graphics, we can write a clamping function as (sample python code):

def clamp(a, b, x):
    if x >= b:
        x = b
    elif x <= a:
        x = a
    return x

In piecewise notation we can notate it as:

\[ \operatorname{clamp}_{a,b}(x)=\begin{cases} a & x\leq a \\ x & a\leq x\leq b \\ b & b\leq x \end{cases}\]

In this sense, it's still important to realise the continuity (you can also, should you opt to, plug this into our original sticking function and you'll get itself out)

We can also re-notate our respective closed and open formulas using this notation:

\[ f(x)=\sum_{k=1}^{n}{f_{k}(\operatorname{clamp}_{s_k,s_{k+1}}(x))}-\sum_{k=2}^{n}f_k(s_k)\]

\[ f(x)=\lim_{m\to\infty}\sum_{k=1}^{n}{f_{k}(\operatorname{clamp}_{s_k,s_{k+1}}(x))}-\sum_{k=2}^{n}f_k(s_k)\]

On a final note, we also have these identities for the clamp function, on \(\mathbb{R}\) (written explicitly):

\[ \lim_{n\to\infty}{\operatorname{clamp}_{-n,a}(x)} = \min(x,a) \\ \lim_{n\to\infty}{\operatorname{clamp}_{a,n}(x)}=\max(x,a)\]

This can be observed in piecewise form or via the absolute-value definition.

(Added and written, 10th of July, 2021)