A piecewise programming problem

Introduction

It's been a little while. I have a job™ now, which unfortunately doesn't afford many opportunities for interesting piecewise problems; so when they do happen, I want to post about them. This post details the time where my colleague is given a problem and needs to solve it (gosh, so generic).

In other news, I've said bye to university. Uni + full-time work is an absolute killer and while I absolutely enjoy the maths university has to give, and that it's still on the radar - it's definitely not something I can juggle at the minute. Back to my own devices I guess!

The problem

We're given the following problem: Given a circle, split up into \(n\) sectors, and a per-sector rotation of \(r\) radians, determine the index of the sector whose region includes the ray \(R\) (with angle \(a_R\)) extending from the centre of the circle with an angle of \(0\) radians.

Visually, this coincides with the Wheel of Fortune, though not exactly.

The solution

We can solve this problem fairly well, with an adapted solution (the original courtesy of aforementioned colleague):

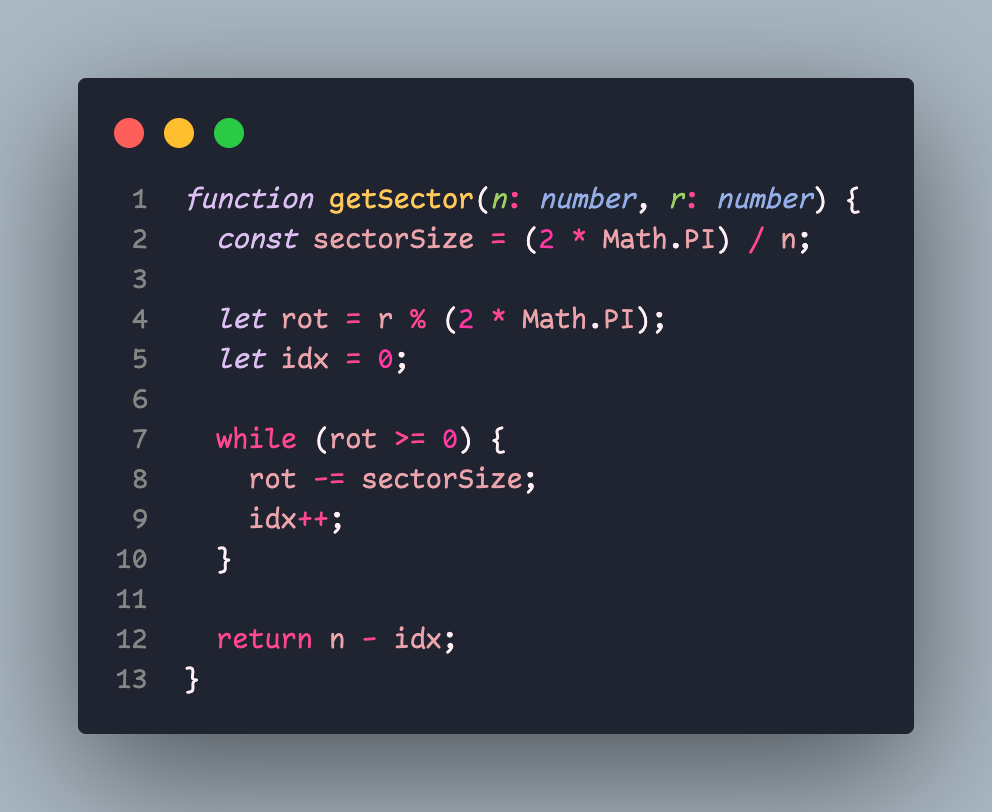
We firstly ensure \(\text{rot}\in[0,2\pi)\). We can then 'subtract' sectors until such point we contain \(R\); such a point exists as we have finite sectors. You will notice that if we have 0 exactly, we will return subtract one further time.

The number of times we subtract is not the intersecting sector; rather, it's the number of sectors we rotated by to get to the current sector. So, for example, if we've rotated by '\(1\) sector', the \(n-1\) sector actually contains \(R\). Had we rotated by \(-1\) sector, the \(0\) sector would contain \(R\)... and so on (Python enthusiasts rejoice for your negative indices have been validated). A reminder that rotating by a sector means rotating by \(\frac{2\pi}{n}\) radians.

Indeed the index of the sector we need can be given by \(n-\text{idx}\) as per the code above.

This algorithm is actually pretty neat wrapped up and could exist on its own forever pretty nicely. However, it's clear it could be a purely mathematical calculation - but how would we find a formula that describes it?

The mathematical solution

We'll begin by making an assumption; let \(r\in[0,2\pi)\). Then the angle, \(a_i\), of each ray that falls within the \(i\) sector can be given by an interval:

\[ a_i\in\left[\left(\frac{2\pi}{n}\right)\cdot i+r,\left(\frac{2\pi}{n}\right)\cdot (i+1)+r\right)\]

From before, there exists a sector such that \(a_R=a_i\). Convince yourself, then, that there exists some \(i\) such that:

\[ \left(\frac{2\pi}{n}\right)\cdot (i+1)+r \geq 2\pi\]

That is, after the rotation \(r\), the upper bound of at least one sector must exceed, or be equal to, \(2\pi\) radians (there is, however, no such guarantee for the lower bound!).

This is the upper-bound of the interval for \(a_i\). We might rearrange this inequality for \(i\):

\[ i\geq \left(1-\frac{r}{2\pi}\right)\cdot n-1\]

As a quick sanity check, recall \(r\in[0, 2\pi)\) and thus the right hand side of this inequality is in the interval \((-1,n-1]\).

We know that \(i\in\mathbb{Z}^+\cup\{0\}\) and we wish to minimise it. One such \(i\) can be given by:

\[ i = \left\lceil \left(1-\frac{r}{2\pi}\right)n\right\rceil-1\]

Now, \(i\in\{0,1,\dots,n-1\}\) as desired.

Solution verification

Recall the piecewise definition of the ceiling function:

\[ \lceil x\rceil=\left\{n+1,\quad x\in(n,n+1]\mid n\in\mathbb{Z}\right\}\]

We can substitute the above expression into our definition:

\[ \begin{align*} \left\lceil \left(1-\frac{r}{2\pi}\right)n\right\rceil &= \left\{m+1,\quad \left(1-\frac{r}{2\pi}\right)n\in(m,m+1]\mid m\in\mathbb{Z}\right\} \\ &= \left\{m+1,\quad 2\pi-r\in\left(\frac{2m\pi}{n},\frac{2(m+1)\pi}{n}\right]\mid m\in\mathbb{Z}\right\} \\ &= \left\{m+1,\quad r\in\left[\frac{2(n-m-1)\pi}{n},\frac{2(n-m)\pi}{n}\right)\mid m\in\mathbb{Z}\right\} \end{align*}\]

Regard that \(r\) is constrained to \([0,2\pi)\). The minimum \(r=0\) is given when \(\frac{2(n-m-1)\pi}{n}=0\iff m=n-1\) and similarly \(r=2\pi\) occurs when \(\frac{2(n-m)\pi}{n}=2\pi\iff m=0\). Therefore we have a further simplification on the values of \(m\):

\[ \left\{m+1,\quad r\in\left[\frac{2(n-m-1)\pi}{n},\frac{2(n-m)\pi}{n}\right)\mid m\in\left\{0,1,\dots,n-1\right\}\right\}\]

This bears incredible resemblance to the roots of unity; indeed, the \(n\text{th}\) roots of unity. We describe \(m+1\) for which \(r\) lies in the \(((n-1)-m)\text{th}\) root; this makes sense, as we reverse the order of the sectors as we rotate, giving us the 'opposite' sector. Further regard that \(i\), our desired index, is precisely \(m\) - as required.